Metadata

作者: Louis Airale, Antonio Longa, Mattia Rigon, Andrea Passerini, Roberto Passerone
日期: 2025
出处: ICML
PDF: https://openreview.net/pdf?id=t3zwUqibMq
开源代码: https://github.com/LouisBearing/Graph-SPSE-Encoding

摘要

图变换器将全局自注意力机制扩展到图结构数据，在图学习领域取得了显著成功。最近，相对随机游走概率（RRWP）被发现通过将结构和位置信息编码到边表示中，能够进一步增强图变换器的预测能力。然而，RRWP并不总能区分属于不同局部图模式的边，这降低了其捕获图完全结构复杂性的能力。本文引入了简单路径结构编码（SPSE），一种利用简单路径计数进行边编码的新方法。我们从理论和实验上证明了SPSE克服了RRWP的局限性¹，提供了更丰富的图结构表示，特别是在捕获局部循环模式方面。为了使SPSE在计算上可行，我们提出了一个简单路径计数的有效近似算法。在各种基准测试中，包括分子图和长程图数据集，SPSE相比RRWP展示了显著的性能提升，在区分性任务中取得了统计显著的增益。这些结果表明SPSE是一种强大的边编码替代方案，可用于增强图变换器的表现力。

研究问题

本文主要研究图变换器(Graph Transformers)中的结构编码问题，特别是针对边表示的设计方法。传统图神经网络(GNNs)依赖局部消息传递机制，难以捕获长程依赖和结构模式。图变换器通过全局自注意力克服了这一限制，但面临着如何设计合适的结构和位置编码的挑战，特别是要捕获图的不规则结构特性。近期研究发现相对随机游走概率(RRWP)可以将结构和位置信息编码到边表示中，增强预测能力。然而，RRWP在某些情况下无法区分属于不同局部图模式的边，限制了其捕获图完全结构复杂性的能力。

RRWP存在的问题

局限性一：无法区分不同图结构的边

RRWP(相对随机游走概率)基于随机游走概率的边编码在某些情况下无法区分来自不同拓扑图结构的边，导致它们为非常不同的图结构分配相同的转换概率。
数学定义：

随机游走矩阵：给定图 $G$ 和 $k ∈ N^*$ ，$k$ 步随机游走矩阵 $P^k ∈ R^{|V|×|V|}$ 给出所有节点对间长度为 $k$ 的随机游走的着陆概率： $P^k = (D^{-1}A)^k$ 其中 $D$ 是度矩阵， $A$ 是邻接矩阵。
等价关系定义：对于 $k ≥ 1$ ， $(i, j)_G =^k_{RW} (i', j')_G' ⇐⇒ (P^k)_{ij} = (P'^k)_{i'j'}$
其中 $P’^k$ 是图G’的k步随机游走矩阵。
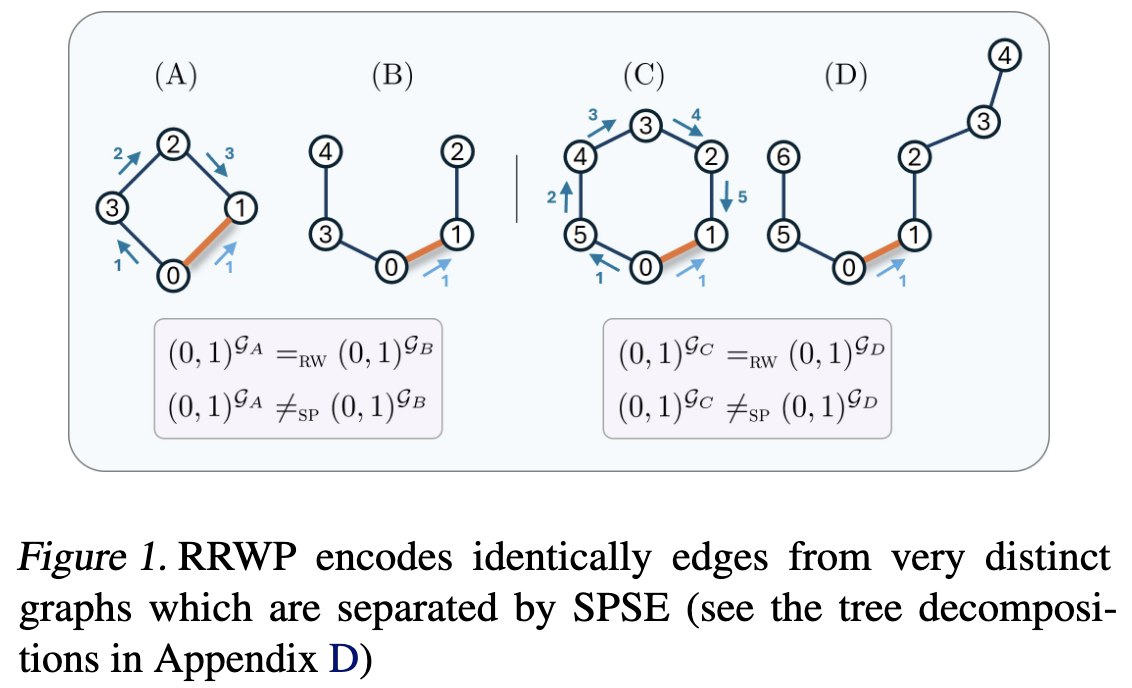
命题1：令 $G = (V, E)$ 是一个偶长度循环图，即 $|V| = 2n$ ，且 $G’ = (V’, E’)$ 是一个路径图，满足 $|V’| = 2n + 1$ 。那么对于G中任意节点对(i, j)，在G’中存在节点对(i’, j’)，使得 $(i, j)_G =^RW (i’, j’)_G’$ 。
这个命题表明，随机游走转换概率无法区分偶长度循环图和路径图，在考虑单节点对时二者是等价的。这意味着RRWP编码可能错过关键的结构差异。
局限性二：缺乏唯一性
命题2：令 $G = (V, E)$ 是一个图，$(i, j) ∈ V × V$ 是一对节点。那么存在一个非同构图 $G’ = (V’, E’)$ 和节点对 $(i’, j’) ∈ V’ × V’$，使得 $(i, j)_G =^RW (i’, j’)_G’$ 。
这表明RRWP编码对于节点对从来不是唯一的，不能用于标识图。

数学公式推导

RRWP等价性的证明概要

命题1的证明使用了表示距离的符号 $pk(j)$ ，表示在循环图G中任意两个相距 $j≤n$ 的节点之间的 $k$ 步游走概率。在线性图G’中，使用节点索引表示与中心节点的距离，$p’k(j)$ 表示从中心节点到距离为j的节点的k步游走概率。
证明分为两个主要部分：

对于所有 $1 ≤ j < n$ 和所有 $k ∈ N^*$ ，证明 $p’k(j) = pk(j)$ ，且 $p’k(n) = 1/2 pk(n)$
证明 $pk(n) = p’k(n,0)$ 对于所有 $k ≥ 1$ 成立，或者等价地，从先前结果有 $p’k(n,0) = 2p’k(n)$
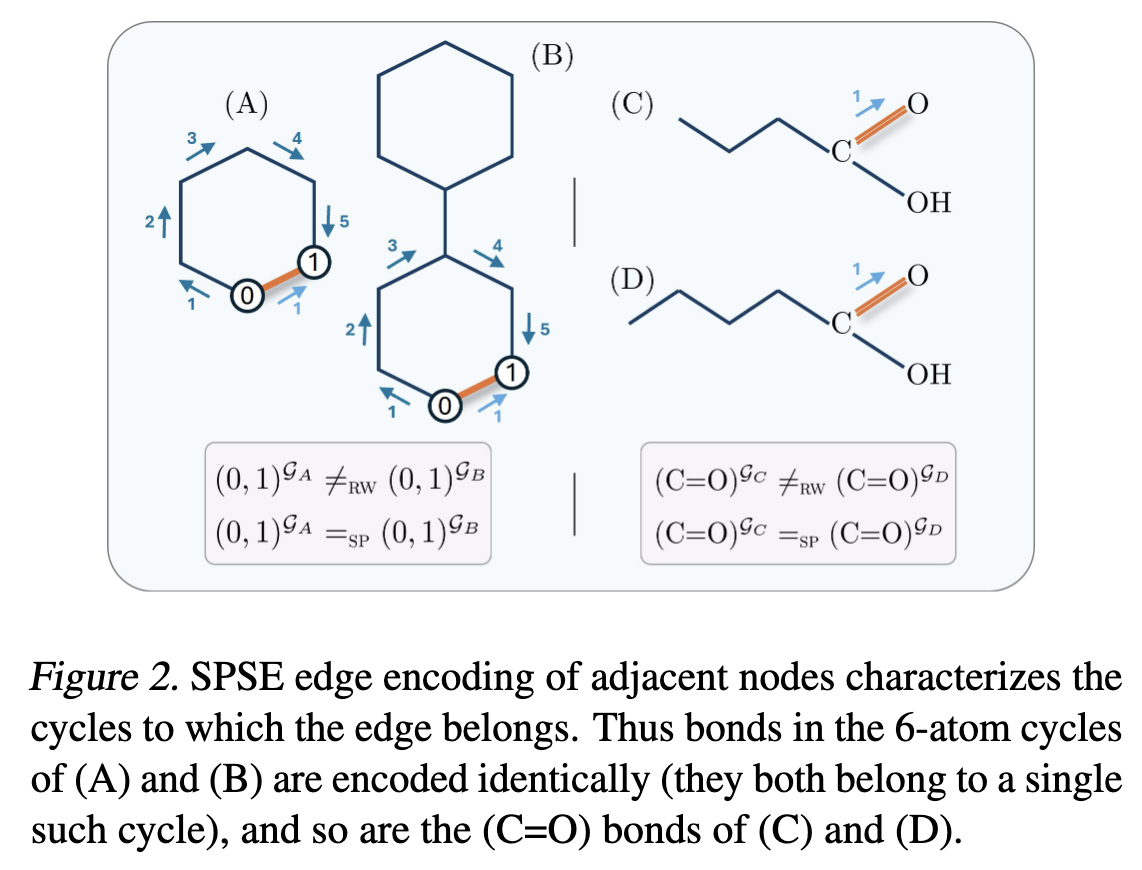
SPSE与循环计数的关系
命题3：令 $(i,j)$ 是图G中的两个相邻节点，即 $(i,j) ∈ E$ ，且 $S^k$ 是G的k步简单路径矩阵， $(S^k)_{ij} = m_k ∈ N$ 。那么对于 $k ≥ 2$ ，G中恰好有 $m_k$ 个长度为 $k+1$ 的循环，它们接受 $(i,j)$ 作为边。
证明：
这个命题可以直接证明。每个包含边 $(i,j)$ 的长度为 $k+1$ 的循环是一个 $k+2$ 个节点的游走，形式为 $i, …j, i$ ，其中只有第一个节点被重复。将其限制到前 $k+1$ 个节点时，其本身是i和j之间长度为k的一条路径，因此增加了 $(S^k)_{ij}$ 。反过来， $(S^k)_{ij}$ 中计数的所有路径都可以通过边ji来完成，形成一个长度为k+1的循环，这证明了等式。
SPSE的路径计数编码函数
SPSE使用对数函数组合来映射路径计数： $f : x \mapsto \alpha g^n(x) + \beta$ 其中$g : x \mapsto \ln(1 + x)$，$\alpha$、$\beta$和$n$是超参数。
归一化的路径计数 $f(S)$ 可以替代随机游走矩阵P作为图变换器模型的边编码输入，产生SPSE矩阵 $E^{SPSE}$ ，用于自注意力机制。

方法

方法概述

Airale等人(2025)在论文中提出了一种称为简单路径结构编码(Simple Path Structural Encoding, SPSE)的新方法，用于图变换器的边结构编码。这种方法通过计算节点间不同长度的简单路径数量来编码图结构信息，为图结构提供了比随机游走概率(RRWP)更丰富的表示，特别是在捕获局部循环模式方面具有优势。

数学基础与理论性质

简单路径矩阵定义

给定图 $G = (V, E, X)$，其中 $V$ 是节点集合，$E$ 是边集合，$X$ 是节点特征矩阵。对于 $k \in \mathbb{N}^{*}$，$k$-跳简单路径矩阵 $S^{k} \in \mathbb{N}^{|V| \times |V|}$ 是一个矩阵，其中 $(S^{k})_{ij}$ 是从节点 $i$ 到节点 $j$ 的长度为 $k$ 的简单路径数量。
与随机游走矩阵 $P^{k} = (D^{-1}A)^k$（其中 $D$ 是度矩阵，$A$ 是邻接矩阵）不同，简单路径矩阵 $S^{k}$ 没有闭式解，计算它非常复杂。

Proposition 3：SPSE与循环计数的关系

SPSE方法的核心理论基础是Proposition 3，它建立了简单路径计数和循环计数之间的直接联系：
Proposition 3：令 $(i,j)$ 是图 $G = (V,E)$ 中的两个相邻节点，即 $(i,j) \in E$ ， $S_{k}$ 是 $G$ 的 $k$ -跳简单路径矩阵，对于任意 $k \in \mathbb{N}^{*}$ ，使得 $(S_{k})_{ij} = m_{k} \in \mathbb{N}$ 。那么对于 $k \geq 2$ ，在 $G$ 中恰好存在 $m_{k}$ 个长度为 $k+1$ 的循环，这些循环以 $(i,j)$ 为一条边。
证明：
这个命题可以通过直接观察来证明。每个长度为 $k+1$ 且以边 $(i,j)$ 为其中一条边的循环可以表示为 $i,j,i_1,i_2,...,i_{k-1},i$ 的形式，其中 $j,i_1,i_2,...,i_{k-1}$ 是节点，且所有节点都是唯一的（除了 $i$ ）。限制到该循环的前 $k+1$ 个节点，它本身是一个从 $i$ 到 $j$ 的长度为 $k$ 的简单路径，因此增加了 $(S_{k})_{ij}$ 。反过来， $(S_{k})_{ij}$ 中计数的所有路径都可以通过添加边 $ji$ 来完成一个长度为 $k+1$ 的循环。这证明了等式。

SPSE算法实现

为了解决简单路径计数计算的复杂性，论文提出了一种高效的近似算法，基于有向无向图(DAG)分解的思想。

算法1：所有节点对之间的路径计数（简化版）

1: Parameters: 根节点比例 R, 最大长度 K, 最大DFS深度 DDFS, 最大试验次数 N
2: Input: 无向图 G = (V, E)
3: Output: 路径计数矩阵 M ∈ ℕ^{|V|×|V|×K}
4: M ← 0^{|V|×|V|×K} {初始化计数矩阵}
5: NODES ← DRAWNODES(R, V) {从V中选择R×|V|个节点}
6: for each v in NODES do
7:     DAGS ← DAGDECOMPOSE(G, v, DDFS, N) {获取以v开头的节点排列列表}
8:     for each DAG in DAGS do
9:         M ← UPDATE(M, DAG) {更新总路径计数}
10:    end for
11: end for
12: Return: M

算法1 的目标

这个算法的主要目的是计算图中所有节点对之间不同长度的简单路径数量，并存储在一个三维矩阵 M 中。由于直接计算所有路径的复杂度极高（指数级），算法采用了一种近似策略：只从部分根节点出发，通过有向无环图（DAG）分解来探索路径，从而高效估计路径计数。

算法流程详解

1.初始化阶段

输入：无向图 G = (V, E)（节点集合 V，边集合 E）
参数设置：
- R：根节点比例（比如 R=0.1 表示选择 10% 的节点作为根节点）
- K：最大路径长度（只计算长度 ≤ K 的路径）
- DDFS：最大 DFS 深度（控制深度优先搜索的深度）
- N：试验次数（每个根节点尝试 N 次不同的路径探索）
初始化计数矩阵：
创建一个三维矩阵 M，大小为 |V| × |V| × K，初始值全为 0。
M[i][j][k] 将存储从节点 i 到节点 j 的长度为 k 的路径数量。
2.选择根节点
从所有节点 V 中随机选择 R × |V| 个节点作为根节点（NODES）。
- 例如：如果图有 1000 个节点，R=0.1，则选择 100 个根节点。
- 这样可以减少计算量，同时保持统计意义。
  3.遍历根节点
  对每个选中的根节点 v：
调用 DAG 分解算法（算法2）：
- 以 v 为根节点，对图 G 进行 DAG 分解，得到多个节点排列列表 DAGS。
- 每个 DAG 代表一种从 v 出发的路径探索顺序。
遍历每个 DAG：
- 对每个 DAG，更新路径计数矩阵 M：
  - 如果 DAG 中存在从 i 到 j 的长度为 k 的路径，则 M[i][j][k] += 1。
- 这样，M 会累加所有 DAG 中发现的路径。
  4.返回结果
最终返回路径计数矩阵 M，其中：
- M[i][j][k] 是从节点 i 到节点 j 的长度为 k 的简单路径的估计数量。
- 由于是近似算法，结果可能略低于真实值（但论文证明下界估计是有效的）。
  关键设计思想

近似计算：
- 不枚举所有可能的路径（计算量太大），而是从部分根节点出发，通过 DAG 分解探索路径。
- 这样可以在可接受的时间内得到合理的估计。
DAG 分解的作用：
- 将无向图转化为有向无环图，避免重复计算和循环路径。
- 结合 DFS 和 BFS（算法2），既能发现长路径，又能覆盖多条分支路径。
参数平衡：
- R 越大，估计越准确，但计算量越高。
- K 越大，能捕获更长路径，但内存需求增加。
- DDFS 和 N 控制探索的深度和多样性。
  举个具体例子
  假设图中有 4 个节点：A, B, C, D，边为 A-B, B-C, C-D, A-D。

参数：R=0.5, K=2, DDFS=1, N=2
流程：
1. 选择根节点（比如 A 和 B）。
2. 对根节点 A：
  - DAG 分解可能得到路径 A→B→C 和 A→D。
  - 更新 M[A][B][1] += 1，M[A][C][2] += 1，M[A][D][1] += 1。
3. 对根节点 B：
  - DAG 分解可能得到路径 B→A→D 和 B→C。
  - 更新 M[B][A][1] += 1，M[B][D][2] += 1，M[B][C][1] += 1。
4. 最终 M 中存储了所有节点对的路径计数估计。
  总结
  算法1 通过随机选择根节点 + DAG 分解 + 路径计数更新，高效地估计了图中所有节点对之间的简单路径数量。虽然结果是近似的，但论文证明这种方法在计算效率和准确性之间取得了很好的平衡，特别适合用于图变换器的结构编码任务。

算法2：DAG分解

1: Parameters: 最大DFS深度 DDFS, 最大试验次数 N
2: Input: 图 G = (V, E), 根节点 r, 直径 DMAX
3: Output: 节点排列列表 Π
4: 初始化 Π ← EmptyList
5: for dDFS = 0 to DDFS do
6:     for n = 1 to N do
7:         初始化 π ← EmptyList
8:         while π ≠ V do
9:             for d = 1 to DMAX do
10:                if d < dDFS then
11:                    π ← DFS(r, G, π) {开始dDFS-1个DFS步骤}
12:                else if d = dDFS then
13:                    π ← PARTIALBFS(r, G, π)
14:                else
15:                    π ← BFS(r, G, π) {尽可能继续多个BFS步骤}
16:                end if
17:            end for
18:        end while
19:        Π ← ADD(Π, π) {将π添加到Π}
20:    end for
21: end for
22: Return: Π

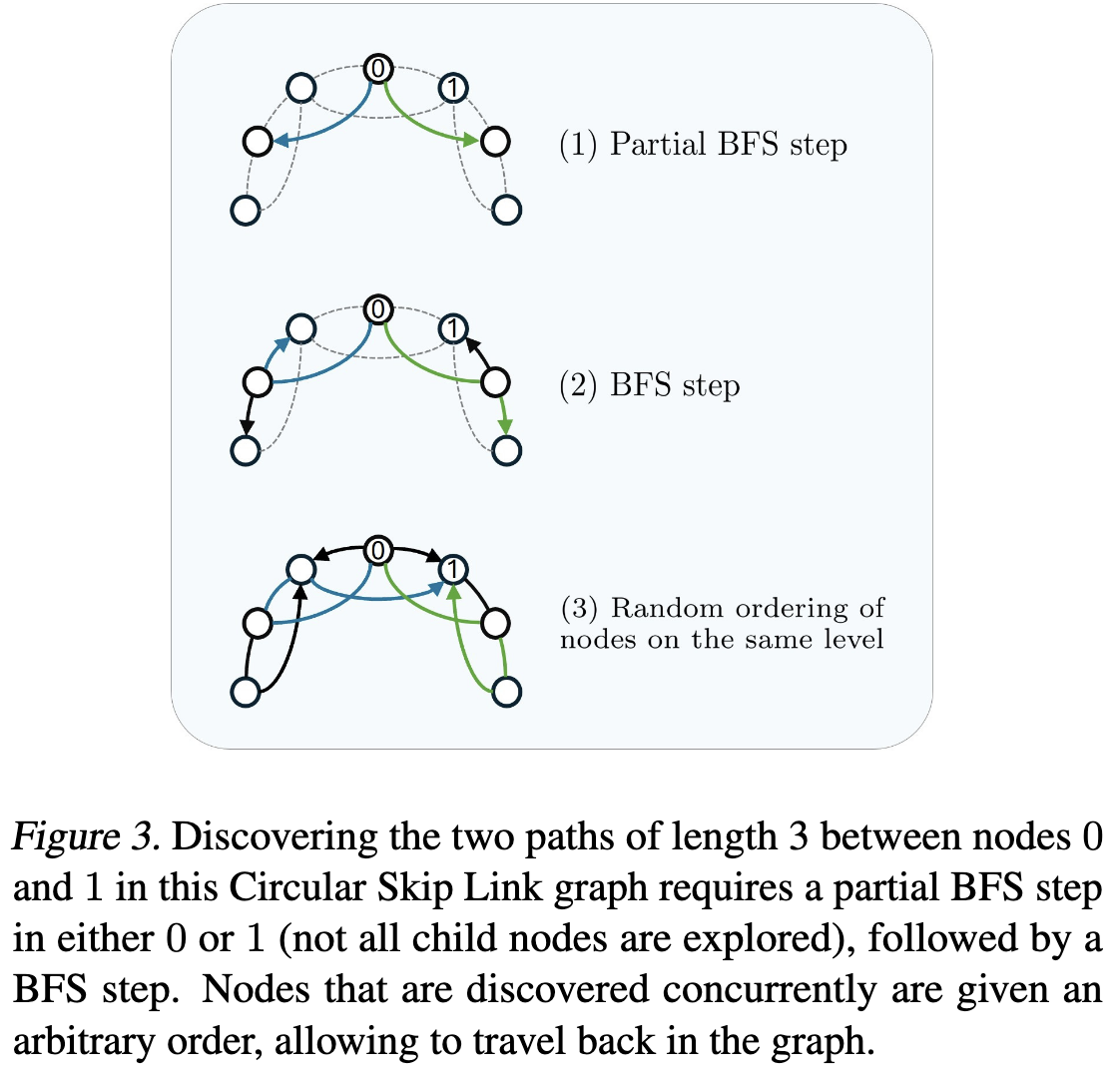
该算法通过结合深度优先搜索(DFS)和广度优先搜索(BFS)来探索不同路径。DFS能够发现长路径，但无法同时发现节点间的多条路径；BFS单独使用通常会遗漏长路径。因此，算法在达到最大DFS深度后切换到BFS，并在中间添加部分BFS步骤，以发现可能被标准DFS和BFS遗漏的路径。

算法2 的目标

这个算法的主要目的是将无向图转化为有向无环图（DAG），并生成一系列节点排列（π），用于后续的路径计数。通过结合深度优先搜索（DFS）和广度优先搜索（BFS），算法能够高效地探索不同长度的路径，同时避免重复计算和循环路径。

算法流程详解

1.初始化阶段

输入：
- 图 G = (V, E)（节点集合 V，边集合 E）
- 根节点 r（路径探索的起点）
- 直径 DMAX（图中最长路径的估计长度）
参数设置：
- DDFS：最大 DFS 深度（控制深度优先搜索的深度）
- N：试验次数（每个 dDFS 值尝试 N 次不同的路径探索）
初始化输出列表：
创建一个空列表 Π，用于存储所有生成的节点排列。
2.双层循环：遍历 DFS 深度和试验次数
外层循环（dDFS 从 0 到 DDFS）：
- 逐步增加 DFS 的深度，从纯 BFS（dDFS=0）到纯 DFS（dDFS=DMAX）。
- 这样可以平衡 DFS 和 BFS 的探索策略。
内层循环（n 从 1 到 N）：
- 对每个 dDFS 值，尝试 N 次不同的路径探索，增加多样性。
  3.路径探索：混合 DFS 和 BFS
  对每次试验（dDFS 和 n 的组合）：
初始化当前排列：
创建一个空列表 π，用于存储当前探索的节点顺序。
循环探索（直到所有节点 V 都被访问）：
- 内层循环（d 从 1 到 DMAX）：
  - 如果 d < dDFS：
    - 执行 DFS 步骤：从当前节点出发，尽可能深地探索路径。
    - 适合发现长路径，但可能遗漏分支路径。
  - 如果 d == dDFS：
    - 执行 部分 BFS 步骤：结合 DFS 和 BFS 的特点，平衡深度和广度。
  - 如果 d > dDFS：
    - 执行 BFS 步骤：从当前节点出发，优先访问所有邻居节点。
    - 适合发现短路径和分支路径，但可能遗漏长路径。
- 更新排列：
  将探索到的节点按顺序添加到 π 中。
- 检查是否完成：
  如果 π 包含所有节点 V，则退出循环。
  4.存储结果
将当前排列 π 添加到输出列表 Π 中。
这样，Π 会包含所有试验生成的节点排列，每个排列代表一种从根节点 r 出发的路径探索顺序。
5.返回结果
最终返回节点排列列表 Π，其中：
- 每个 π 是一个节点排列，表示从根节点 r 出发的一种路径探索顺序。
- 这些排列将用于算法1中的路径计数更新。
  关键设计思想

混合搜索策略：
- DFS 能发现长路径，但可能遗漏分支路径。
- BFS 能发现短路径和分支路径，但可能遗漏长路径。
- 通过调整 dDFS，算法在 DFS 和 BFS 之间取得平衡。
参数控制：
- DDFS 控制最大 DFS 深度，影响路径探索的深度。
- N 控制试验次数，增加路径探索的多样性。
避免循环路径：
- 通过 DAG 分解，将无向图转化为有向无环图，确保路径探索不会陷入循环。
  举个具体例子
  假设图中有 4 个节点：A, B, C, D，边为 A-B, B-C, C-D, A-D，根节点为 A。

参数：DDFS=1, N=2, DMAX=3
流程：
1. dDFS=0（纯 BFS）：
  - 第一次试验：A → B → C → D
  - 第二次试验：A → D → C → B
2. dDFS=1（混合 DFS 和 BFS）：
  - 第一次试验：A → B → C（DFS），然后 A → D（BFS）
  - 第二次试验：A → D → C（DFS），然后 A → B（BFS）
3. dDFS=2（更深的 DFS）：
  - 第一次试验：A → B → C → D
  - 第二次试验：A → D → C → B
4. 最终 Π 包含 6 个节点排列，用于路径计数。
  总结
  算法2 通过混合 DFS 和 BFS 策略，高效地将无向图转化为 DAG，并生成多样化的节点排列。这些排列为算法1中的路径计数提供了丰富的探索顺序，确保了路径计数的准确性和多样性。

算法复杂度

SPSE算法的计算复杂度为 $O(KRDDFSN|V|^3)$，其中：

$K$ 是最大路径长度
$R$ 是根节点比例
$DDFS$ 是最大DFS深度
$N$ 是试验次数
$|V|$ 是节点数量
虽然这比RRWP的计算成本高，但它只需要作为预处理步骤计算一次，并且远小于所有可能DAG分解的数量 $2^{|E|}$，突显了树分解方法的有效性。
路径计数编码
由于节点间的路径数量可能非常大，作者使用对数函数复合将路径计数映射到适合神经网络的值范围： $f: x \rightarrow \alpha g^n(x) + \beta$ 其中 $g: x \rightarrow \ln(1 + x)$，$\alpha$、$\beta$ 和 $n$ 是需要调整的超参数。
这种映射函数 $f$ 能够有效处理大范围的路径计数值，将它们变换到适合神经网络处理的值范围。
SPSE在图变换器中的应用
在图变换器中，SPSE矩阵 $E^{SP}$ 替换了原来的RRWP矩阵 $E^{RW}$。自注意力层的计算可以表示为： $a_{ij} = \phi_1(W_Q x_i, W_K x_j, (E^{SP})_{ij})$ $\alpha_{ij} = \frac{\exp(a_{ij})}{\sum_k \exp(a_{ik})}$ $y_i = \sum_j \alpha_{ij} \phi_2(W_V x_j, (E^{SP})_{ij})$ 其中 $x_i$ 和 $x_j$ 分别是节点 $i$ 和 $j$ 的特征，$W_Q$、$W_K$ 和 $W_V$ 是查询、键和值矩阵，$y_i$ 是自注意力层的输出。
实验结果
论文在多个基准测试上验证了SPSE的有效性：

循环计数合成实验：在包含循环的合成图上，SPSE展现比RRWP显著更高的循环计数准确率，验证了Proposition 3的有效性。
真实世界基准测试：在分子数据集（ZINC, Peptides, PCQM4Mv2）、超像素数据集（MNIST, CIFAR10）和随机块模型（PATTERN, CLUSTER）上，SPSE在21/24的案例中提升了性能，特别是在分子数据集上表现尤为突出。
超参数敏感性分析：研究表明不同数据集对超参数的敏感性各异。分子数据集主要受益于根节点比例 $R$ 的增加，而超像素数据集则从所有超参数的增加中受益。
方法局限性
作者也指出了SPSE的局限性：
高密度图挑战：在高度连接的图中，SPSE的改进有限，因为准确计数路径变得困难。
路径枚举限制：由于内存限制，算法无法枚举所有路径，而是存储下界估计，可能导致某些情况的路径计数不准确。
总之，SPSE通过利用简单路径计数作为边编码，显著提升了图变换器在捕获结构信息方面的能力，特别是在处理分子图和长程依赖关系时表现出色，为图结构表示学习提供了一种更强大的方法。

附录

附录A RRWP算法详解

本文中对比的 RRWP（Relative Random Walk Probabilities，相对随机游走概率）算法 是一种用于 图Transformer（Graph Transformer） 的结构编码（structural encoding）方法。它的主要思想是通过随机游走（random walk）概率矩阵来表示节点之间的结构关系，从而为Transformer的自注意力层提供图结构信息。下面我用通俗的语言和图示来解释它的核心概念、计算方式以及局限性。

一、RRWP的核心思想

在普通Transformer中，位置编码（positional encoding）告诉模型序列中单词的相对位置；
在图Transformer中，我们需要告诉模型节点之间的结构位置关系。
RRWP通过模拟“随机游走”来实现这种结构编码。

“随机游走”可以理解为：从一个节点出发，随机选择一个邻居节点走一步，这样连续走K步，就得到一条随机路径。

RRWP的关键是构造多个不同长度的随机游走概率矩阵：

$P_k = (D^{-1}A)^k$

其中：

$A$：图的邻接矩阵（$A_{ij}=1$表示i与j之间有边）
$D$：节点的度矩阵（$D_{ii}$是节点i的度数）
$D^{-1}A$：一步随机游走的转移概率矩阵
$(D^{-1}A)^k$：从一个节点出发随机走k步，到达另一个节点的概率

我们将这些概率矩阵按步数堆叠起来：

$P = [P_1, P_2, \dots, P_K]$

再通过一个浅层神经网络映射成高维特征：

$E_{RW} = \phi_0(P)$

最后在自注意力计算中，节点对$(i,j)$的注意力不仅取决于它们的特征，还受到对应的结构编码$E_{RW}(i,j)$影响：

$a_{ij} = \phi_1(W_Qx_i, W_Kx_j, E_{RW}(i,j))$

二、RRWP的直观理解

可以将RRWP理解为：
“节点i到节点j之间，通过不同步数的随机游走，到达j的概率是多少？”
例如下图所示：

1
2
3

   (A)
 /  |  \
B - C - D

从A出发：

一步到B、C、D的概率都为 1/3；
两步可能通过不同路径回到自己或走到别的节点；
于是我们能得到一系列概率，反映节点之间的结构“可达性”和“距离”。
三、RRWP的优势
封闭形式（closed form）计算简单：
$(D^{-1}A)^k$ 可以直接矩阵乘法得到。
包含多尺度结构信息：
不同的k对应不同的“跳数”。
可作为Transformer注意力的结构偏置（bias），使模型知道哪些节点在图上更“近”或结构上更相关。
四、RRWP的缺陷
论文中指出，RRWP 无法区分某些结构不同的图，尤其是当局部拓扑差异较小时。
例如：
一个“环形图（cycle）”与一个“直线图（path）”在某些边上，RRWP会给出相同的随机游走概率；
这样模型就无法区分“环”和“链”。
论文给出的理论证明表明：

在偶数长度的环图与相应长度的路径图之间，存在节点对((i,j))，它们的RRWP编码完全相同。

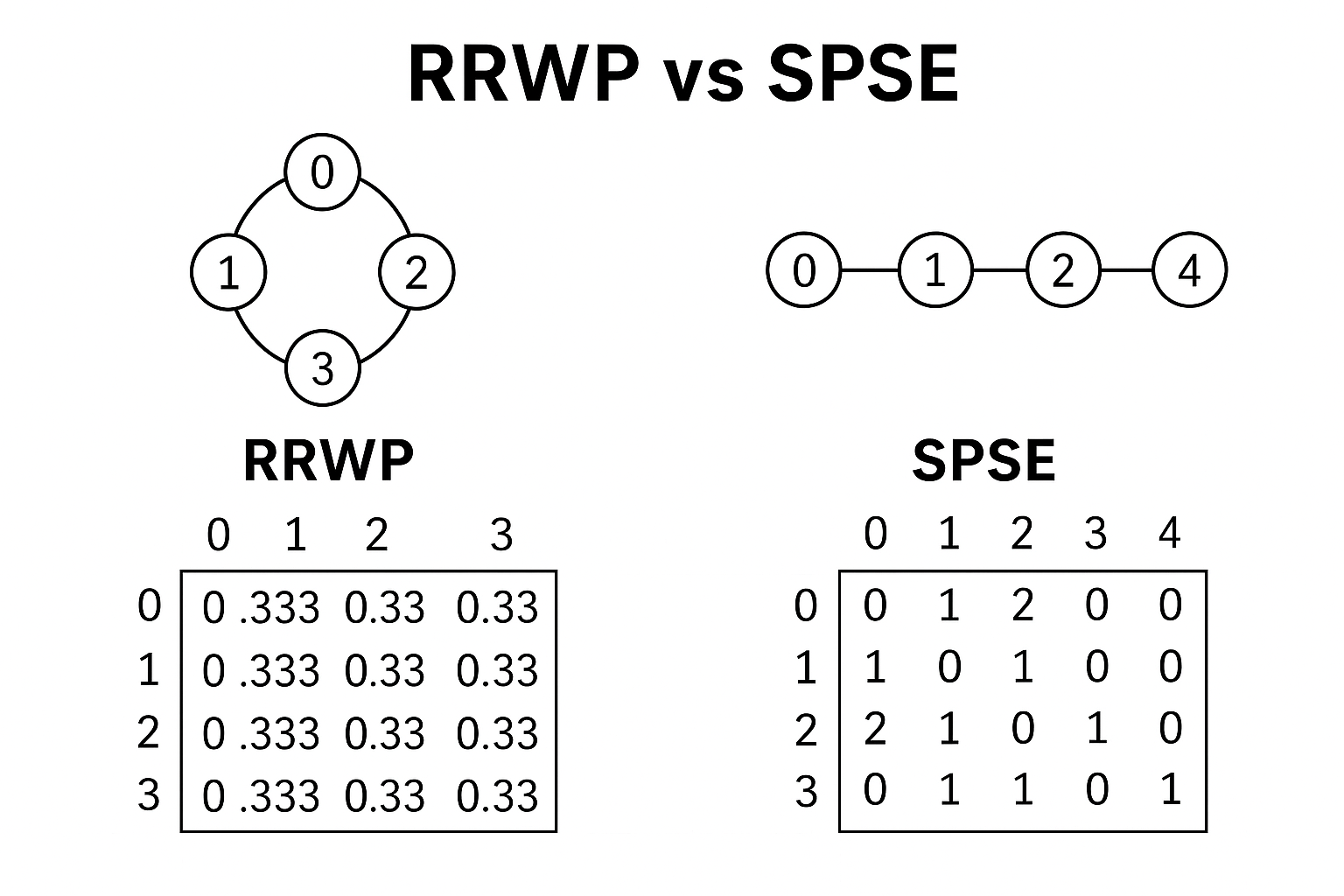
如图示例所示（论文Figure 1）：

1 2	Cycle graph (C4): 0 - 1 - 2 - 3 - 0 Path graph (P5): 0 - 1 - 2 - 3 - 4

RRWP对边(0,1)计算出的概率分布是一样的。

五、RRWP与SPSE（本文方法）的区别示意图

对比项目	RRWP	SPSE（本文提出）
编码依据	随机游走概率（可能重复节点）	简单路径计数（不重复节点）
能否区分环与链	❌ 不能	✅ 能
数学表达	$(P_k = (D^{-1}A)^k)$	$(S_k(i,j))$ ：i到j之间长度为k的简单路径数
优点	快速、闭式解	结构信息更丰富，可捕捉局部循环
缺点	结构歧义（如偶环和路径）	计算复杂度高（需近似算法）

六、RRWP机制示意图

下面是一个直观示意（文本图）：

      图结构：
      1 -- 2 -- 3
       \        /
         \    /
           4
随机游走 (RRWP):
  从1出发：
   1步：到2或4的概率 0.5
   2步：到3的概率 0.5 (经由2或4)
   3步：又能回到1

SPSE (Simple Path):
  只计算不重复节点的路径：
   1→2→3
   1→4→3
  两条简单路径长度为2

RRWP会混淆，因为“1→2→1→4→3” 也算一种随机游走；
而SPSE会忽略这种带重复节点的路径，更准确地反映结构差异。

七、总结

RRWP是图Transformer的一种经典结构编码方案，核心优点是：

简单高效；
能捕获全局结构信息。
但它的本质是概率而非结构计数，因此：
在局部结构（如环 vs 链）上存在模糊性；
不能显式捕捉循环、环状或支路模式。
SPSE正是为了解决这些问题提出的，用“简单路径计数”代替“随机游走概率”，使编码更能反映图的真实结构。
是否希望我给你画出一张RRWP与SPSE的对比示意图（含环形与路径示例）？
我可以用简洁的图示（类似论文Figure 1 + Figure 2）帮你更直观理解为什么RRWP无法区分环和链。

Metadata

摘要

研究问题

RRWP存在的问题

局限性一：无法区分不同图结构的边

局限性二：缺乏唯一性

数学公式推导

RRWP等价性的证明概要

SPSE与循环计数的关系

SPSE的路径计数编码函数

方法

方法概述

数学基础与理论性质

简单路径矩阵定义

Proposition 3：SPSE与循环计数的关系

SPSE算法实现

算法1：所有节点对之间的路径计数（简化版）

算法1 的目标

算法流程详解

1.初始化阶段

2.选择根节点

3.遍历根节点

4.返回结果

关键设计思想

举个具体例子

总结

算法2：DAG分解

算法2 的目标

算法流程详解

1.初始化阶段

2.双层循环：遍历 DFS 深度和试验次数

3.路径探索：混合 DFS 和 BFS

4.存储结果

5.返回结果

关键设计思想

举个具体例子

总结

算法复杂度

路径计数编码

SPSE在图变换器中的应用

实验结果

方法局限性

附录

附录A RRWP算法详解

一、RRWP的核心思想

二、RRWP的直观理解

三、RRWP的优势

四、RRWP的缺陷

五、RRWP与SPSE（本文方法）的区别示意图

六、RRWP机制示意图

七、总结