Metadata

作者: Jiaming Zhuo, Yuwei Liu, Yintong Lu, Ziyi Ma, Kun Fu, Chuan Wang, Yuanfang Guo, Zhen Wang, Xiaochun Cao, Liang Yang
出处: ICLR
PDF: https://openreview.net/pdf?id=4v4RcAODj9
开源代码: https://github.com/JiamingZhuo/DUALFormer

摘要

图变换器(Graph Transformers，GTs)擅长捕获图的全局性和局部性，在节点分类任务中显示出巨大的潜力。大多数最先进的GTs通过将局部图神经网络(GNNs)与全局自注意力(SA)模块相结合来增强结构感知能力，取得了成功。然而，这种架构面临着由可扩展性挑战以及捕获局部和全局信息之间的权衡所导致的限制。一方面，与SA模块相关的二次复杂度对许多GTs构成了重大挑战，特别是当它们扩展到大规模图时。许多GTs需要在表达性和计算效率之间做出妥协。另一方面，GTs在捕获长程依赖的同时保持详细的局部结构信息方面面临挑战。因此，它们通常需要高昂的计算成本来平衡局部和全局表达性。
为了解决这些限制，本文引入了一种新颖的GT架构，称为DUALFormer，其GNN和SA模块具有双维度设计。利用线性化变换器的近似理论并将查询视为节点特征的代理表示，DUALFormer能够在特征维度上高效地执行计算密集型的全局SA模块。此外，通过将局部和全局模块分离到双维度，DUALFormer实现了局部和全局表达性的自然平衡。理论上，DUALFormer可以减少类内方差，从而增强节点表示的判别性。在十一个真实数据集上的广泛实验证明了其相对于现有最先进GTs的有效性和效率。

研究问题

研究的核心问题

1. 可扩展性问题

现有的图Transformer，特别是基于传统自注意力机制(Self-Attention, SA)的模型，面临严重的可扩展性挑战。Zhuo 等 (2025) 指出，自注意力模块的二次方复杂度( $O(n²)$ )使得很多图Transformer难以扩展到大规模图。为了解决这个问题，现有方法通常需要做出妥协——要么牺牲一定的全局表达性(如NAGphormer和Exphormer)，要么增加模型复杂度(如GOAT和CoBFormer)，导致模型泛化能力受限。

2. 局部性与全局性的权衡困境

第二个主要挑战是图Transformer在捕获局部结构和全局依赖信息之间的权衡。现有的图Transformer难以在保留详细局部结构信息的同时捕获长距离依赖关系。这导致它们通常需要显著的计算成本来平衡局部和全局表达能力。Zhuo 等 (2025) 特别指出，一些最先进的图Transformer(如NAGphormer、GOAT、SGFormer、Polynormer和CoBFormer)仍然依赖于GNN来学习局部节点表示，然后将这些表示与自注意力块结合生成最终节点表示，但这种融合会导致信息损失。

解决方案

为解决上述问题，Zhuo 等 (2025) 提出了DUALFormer，一种具有双维度设计的创新图Transformer架构。主要创新点包括：

双维度设计：将GNN和SA模块分别部署在不同维度上，在节点维度上建模局部信息，在特征维度上建模全局信息。
高效全局注意力：利用线性化Transformer的近似理论，将查询(Q)视为节点特征的代理表示，在特征维度上高效执行计算密集的全局SA模块。
自然平衡局部与全局：通过在双维度上分离局部和全局模块，自然地平衡了局部和全局表达能力。

论文通过理论分析证明，DUALFormer可以减少类内方差，增强节点表示的判别性。在11个真实世界数据集上的广泛实验验证了DUALFormer在效果和效率上均优于现有的最先进图Transformer。

综上所述，本论文主要研究的是解决现有图Transformer在可扩展性和局部-全局信息权衡方面的局限性，并提出了一种创新的、双维度设计的解决方案DUALFormer。

方法

1. 方法整体架构

DUALFormer的核心创新在于其双维度设计，将传统的局部GNN模块和全局SA模块分别从节点维度和特征维度解耦，形成以下架构：

输入投影层：将原始节点属性投影到低维空间
全局注意力模块：在特征维度捕获全局依赖关系
局部图卷积模块：在节点维度捕获局部结构信息

全流程如下：

    graph TD
    A["输入节点属性X"] --> B["输入投影层MLP(X) = H0"]
    B --> C{"全局注意力模块<br/>Global Attention Module"}
  
    subgraph 全局注意力层["Global Attention Layers"]
        direction LR
        C --> D["计算查询、键、值Q = H·Wq K = H·Wk V = H·Wv"]
        D --> E["计算特征间注意力矩阵M = softmax(Q⊤K/√n)"]
        E --> F["更新节点表示~Z = V·M"]
        F --> G["残差连接Z = α·~Z + (1-α)·H"]
    end
  
    G --> H{"局部图卷积模块Local Graph Convolution Module"}
  
    subgraph 局部卷积层["GNN Layers"]
        direction LR
        H --> I["应用图卷积H = GNN(A, Z)"]
        I --> J["残差连接H = H + prev_H"]
    end
  
    J --> K["输出预测Y = MLP(H)"]
  
    style B fill:#f9f,stroke:#333,stroke-width:2px
    style C fill:#bbf,stroke:#333,stroke-width:2px
    style H fill:#bfb,stroke:#333,stroke-width:2px
    style K fill:#fbb,stroke:#333,stroke-width:2px

2. 数学公式与推导

2.1 输入投影层s

首先使用前馈网络(FFN)将原始节点属性 $X∈R^{(n×f)}$ 投影到低维隐藏空间：

$H^0 = \text{MLP}(X)$

其中 $n$ 是节点数， $f$ 是原始特征维度， $MLP$ 代表多层感知机。

2.2 全局注意力模块

这是DUALFormer的核心创新。与传统GT在节点维度计算自注意力不同，DUALFormer在特征维度计算全局自注意力，将复杂度从 $O(n²)$ 降低到 $O(f²)$ 。
查询(Q)、键(K)、值(V)计算：

$Q^{(l)} = \hat{Z}^{(l-1)} W_Q^{(l)}$ $K^{(l)} = \hat{Z}^{(l-1)} W_K^{(l)}$ $V^{(l)} = \hat{Z}^{(l-1)} W_V^{(l)}$

其中 $W_Q^{(l)}$ , $W_K^{(l)}$ , $W_V^{(l)} \in \mathbb{R}^{d \times d}$ 是可学习的投影矩阵。
特征维度注意力计算：

$M^{(l)} = \text{softmax}\left(\sigma(Q^{(l)})^T K^{(l)} / \sqrt{n}\right)$ $\tilde{Z}^{(l)} = V^{(l)} M^{(l)}$ $\hat{Z}^{(l)} = \alpha \tilde{Z}^{(l)} + (1-\alpha) \hat{Z}^{(l-1)}$

这里 $σ$ 是激活函数(如 $softmax$ )， $M∈R^{(d×d)}$ 是特征间注意力分数矩阵， $α$ 是超参数用于平衡当前层和前一层。

2.3 局部图卷积模块

在获得全局表示后，使用图神经网络模块整合局部信息：

$\hat{H}^{(k)} = \text{GNN}(A, \hat{H}^{(k-1)})$

其中 $\hat{H}^{(0)} = \hat{Z}^{(L)}$ ， $L$ 是注意力层数，GNN可选择SGC等实现：

$\text{SGC}(A, H) = \hat{A}H$

其中 $\hat{A} = D^{-1/2}(A+I)D^{-1/2}$ 是归一化的邻接矩阵。
预测层：

$\hat{Y} = \text{MLP}(\hat{H}^{(K)})$

3. 理论分析

定理1: 判别性改进

全局注意力模块可以减少类内方差，同时保持类间方差不变。
推导过程：
设节点特征 $x_v \in \mathbb{R}^f$ 为列向量。根据方差分解:

$\text{Var}[X] = \mathbb{E}[\text{Var}[X|Y]] + \text{Var}[\mathbb{E}[X|Y]]$

其中 $\text{Var}[X|Y=k]$ 表示第k类的方差， $\mathbb{E}[X|Y=k]$ 表示第 $k$ 类的中心。
对于全局注意力模块，变换后的特征为 $M^T x_v$ ，对应的随机变量为 $M^T X$ 。
结论1：类内方差满足

$\mathbb{E}[\text{Var}[M^T X|Y]] \leq \mathbb{E}[\text{Var}[X|Y]]$

结论2：如果注意力矩阵M满足 $\|e_i - e_j\|_2\leq\varepsilon$ （当 $M_{ij} \neq 0$ 时），则：

$\|\hat{e}_j - e_j\|_2 \leq \varepsilon$

其中 $e_j$ 和 $\hat{e}_j$ 分别是变换前后的类中心。
这表明有效的特征注意力可以减少类内方差，同时保持类间距离相对不变，从而提高节点表征的判别性。

4. 方法优势与解释

4.1 高效可扩展性

传统GT使用节点自注意力 $(sim(Q,K)∈R^(n×n))$ ，复杂度为 $O(n²)$ 。而DUALFormer在特征维度计算注意力 $(M∈R^(d×d))$ ，复杂度为 $O(fd)$ ，且通常 $f << n$ ，实现了线性复杂度 $O(n)$ 。

4.2 局部与全局信息的自然融合

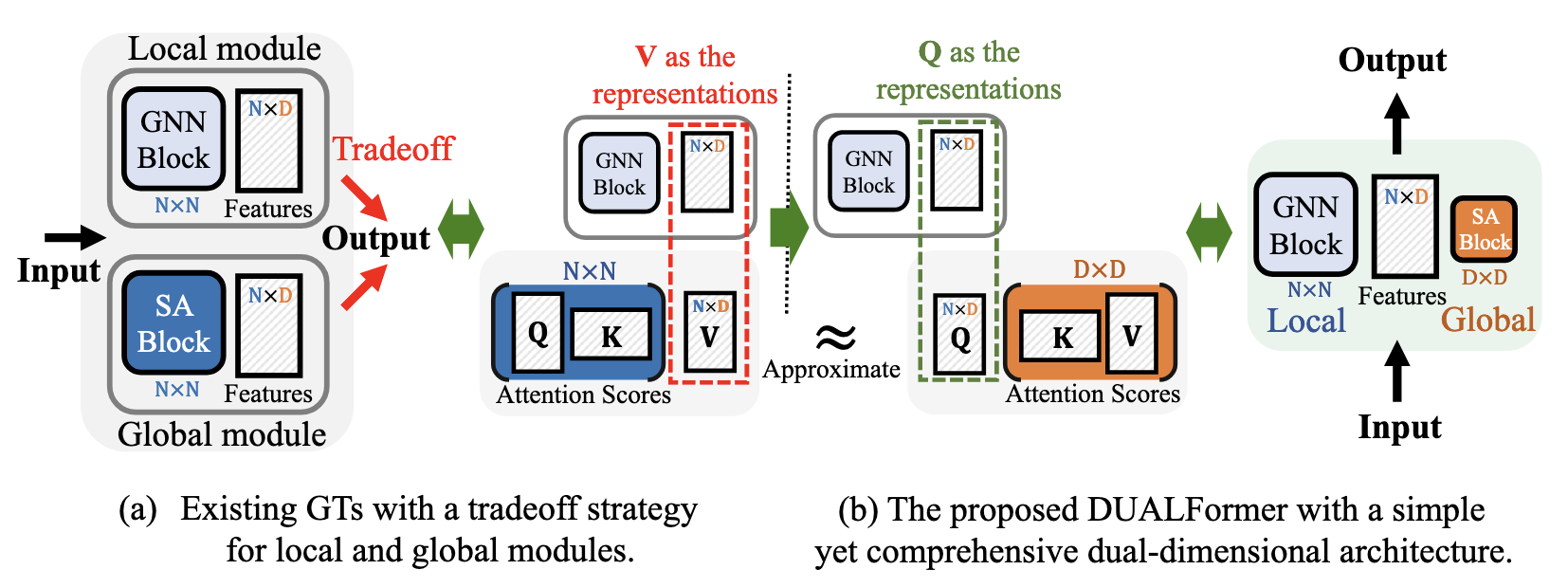
传统GT如图1(a)所示，需在节点维度权衡局部(GNN)和全局(SA)信息，容易导致信息丢失。而DUALFormer(图1(b))将两个维度解耦：

节点维度：GNN捕获局部结构信息
特征维度：SA捕获全局相关性

通过 $(Q×K)^T × V ≈ Q × (K^T × V)$ 的近似理论，实现了全局依赖与局部信息的平衡，避免传统权衡困境。

4.3 设计简洁性

相比现有GT(如表1所示)常需要位置编码、增强训练损失或额外参数，DUALFormer仅使用简单的局部图卷积和全局注意力，架构更加精简高效。

5. 实验验证

DUALFormer在7个节点分类任务(表2)和4个节点属性预测任务(表3)上展现了优越性能。例如，在Cora和PubMed上分别达到85.88%和83.97%的准确率，显著超越基线模型。同时，实验证明其具有线性扩展能力(图3)和参数稳定性(图5-6)。
综上所述，DUALFormer通过创新的双维度设计，有效解决了图变换器的可扩展性和局部与全局信息权衡问题，在节点分类和属性预测任务上展现出了优异的性能和效率。

附录

1.DUALFormer注意力模块详解

1. 注意力模块概述

DUALFormer中的全局注意力模块(Global Attention Module)是设计的核心组件之一，其创新之处在于在特征维度而非传统节点维度上执行自注意力机制。这种设计有效解决了现有图变换器(GT)的两个主要挑战：可扩展性和局部性与全局性之间的权衡问题。

2. 数学公式与推导

2.1 标准自注意力与线性化注意力分析

标准自注意力机制

$\hat{z}_v = \sum_{u \in V} \frac{\exp(\text{sim}(q_v, k_u))}{\sum_{u \in V} \exp(\text{sim}(q_v, k_u))} v_u$

在向量形式下:

$\hat{Z} = \text{Sim}(Q, K)V$

标准自注意力将值(V)作为节点特征的代理表示，注意力分数矩阵 $\text{Sim}(Q, K)$ 作为节点间依赖矩阵，实现全局节点间消息传递。

线性化自注意力机制

$\hat{Z}_v = \phi(q_v) \frac{\sum_{u \in V} \phi(k_u)^T v_u}{\sum_{u \in V} \phi(k_u)^T}$

在向量形式下:

$\hat{Z} = \phi(Q)\phi(K)^T V$

线性化自注意力将查询 $\phi(Q)$ 视为Z的表示，将乘积矩阵 $\phi(K)V$ 视为特征之间的相关矩阵，实现特征间的消息传递。

2.2 全局注意力模块实现

DUALFormer的全局注意力模块按以下步骤实现:

2.2.1 查询、键、值投影

$Q^{(l)} = \hat{Z}^{(l-1)} W_Q^{(l)}, \quad K^{(l)} = \hat{Z}^{(l-1)} W_K^{(l)}, \quad V^{(l)} = \hat{Z}^{(l-1)} W_V^{(l)}$

其中 $W_Q^{(l)}, W_K^{(l)}, W_V^{(l)} \in \mathbb{R}^{d \times d}$ 是可学习投影矩阵。

2.2.2 注意力分数矩阵计算

$M^{(l)} = \text{softmax}\left(\frac{(Q^{(l)})^T K^{(l)}}{\sqrt{n}}\right)$ $M \in \mathbb{R}^{d \times d}$

是低维注意力分数矩阵，表征特征-特征相关性，其维度远小于传统的 $n\times n$ 节点注意力矩阵。

2.2.3 注意力应用

$\tilde{Z}^{(l)} = V^{(l)} M^{(l)} = V^{(l)} \text{softmax}\left(\frac{(Q^{(l)})^T K^{(l)}}{\sqrt{n}}\right)$

2.2.4 残差连接与平衡

$\hat{Z}^{(l)} = \alpha \tilde{Z}^{(l)} + (1 - \alpha) \hat{Z}^{(l-1)}$

其中 $\alpha$ 是平衡注意力和前一层表示的超参数。

2.3 多头注意力扩展

为了增强表示能力，DUALFormer可以融入多头注意力机制:

$\hat{Z}_{\text{final}} = \text{Concat}(\hat{Z}^{(0)}, \hat{Z}^{(1)}, \ldots, \hat{Z}^{(t-1)}) W_O$

其中 $t$ 是头的数量， $W_O \in \mathbb{R}^{td \times d}$ 是可学习投影矩阵。

3. 理论分析与优势

3.1 判别性改进定理

定理1. 全局注意力模块减少类内方差同时保持类间方差不变。
证明:
假设节点特征 $x_v$ 和标签 $y_v$ 是随机变量 $X$ 和 $Y$ 的观测值，且节点特征是均值为零的: $E[X] = 0$ 。根据总方差定律:

$\text{Var}[X] = E[\text{Var}[X|Y]] + \text{Var}[E[X|Y]]$

全局注意力的关键节点特征变换是 $XM$ ，其中 $M = [m_{ij}] = \text{softmax}(Q^T K/\sqrt{n})$ 是特征间的随机矩阵。
经过全局注意力后，节点特征变为 $M^T x_v \in \mathbb{R}^f$ 。通过推导可以证明两个关键性质:

类内方差减少: $E[\text{Var}[M^T X|Y]] \leq E[\text{Var}[X|Y]]$
类间方差保持:
如果学习的注意力矩阵足够好，使得对于任何 $m_{ij} \neq 0$ 有 $\|e_i - e_j\|_2 \leq \varepsilon$ ，则: $\|\hat{e}_j - e_j\|_2 \leq \varepsilon$ 其中 $\varepsilon$ 可以适当选择 $M$ 而变得任意小。

3.2 特征注意力与节点注意力的对比

效率对比

节点注意力复杂度: $O(n^2)$ ，其中 $n$ 是节点数量
特征注意力复杂度: $O(f^2)$ ，其中 $f$ 是特征维度

由于通常 $f \ll n$ ，特征注意力显著提高了计算效率。

性能对比

特征注意力缓解了有限训练数据和大规模复杂关系建模之间的冲突:

节点注意力需要精确建模 $n^2$ 对关系，但图上训练数据通常不足以支撑如此大规模的训练
特征注意力只需建模 $f^2$ 对关系，训练需求大幅降低

4. 实际应用意义

DUALFormer的注意力模块通过在特征维度上建模全局依赖关系，实现了:

高效可扩展的计算，线性时间复杂度 $O(n + e)$
自然平衡局部与全局表达能力，避免传统GT中的权衡困境
降低类内方差，提高节点表示的判别性
减少对额外组件(如位置编码、增强训练损失)的依赖，简化模型架构

通过这种创新的双维度设计，DUALFormer能够在保持全局表达能力的同时，显著提升计算效率和模型性能。

References

NAGphormer: A Tokenized Graph Transformer For Node Classification In Large Graphs