摘要

图变换器需要强归纳偏置来推导有意义的注意力分数。然而，当前方法往往难以捕获更远的距离、层次结构或社区结构，而这些结构在各种图中都很常见，如分子图、社交网络和引用网络。本文提出了一种层次距离结构编码（Hierarchical Distance Structural Encoding, HDSE）方法，用于模拟图中的节点距离，重点关注其多级层次性质。我们引入了一个新框架，将HDSE无缝集成到现有图变换器的注意力机制中，允许与其他位置编码同时应用。为了将带有HDSE的图变换器应用于大规模图，我们进一步提出了一种高级HDSE，有效将线性变换器偏向图的层次结构。我们从理论上证明了HDSE在表达能力和泛化能力方面的优越性。实验上，我们证明了带有HDSE的图变换器在图分类、7个图级别数据集的回归任务以及11个大规模图的节点分类任务中表现出色。

研究问题

研究问题概述

Luo等(2024)指出，图变换器需要强大的归纳偏置(inductive biases)来获得有意义的注意力得分，但现有方法存在以下几个关键问题：

层次结构捕捉不足：当前方法往往难以捕捉图中的长距离、层次结构或社区结构，而这些结构在分子图、社交网络和引用网络等各类图中普遍存在。
与MPNNs对比的局限性：与消息传递图神经网络(MPNNs)相比，图变换器虽然能避免MPNNs的过度平滑(oversmoothing)和过度压缩(over-squashing)问题，但缺乏强归纳偏置。
位置编码挑战：发展有效的位置编码具有挑战性，因为图数据中的层次结构识别与其他欧几里得域有显著差异，导致图变换器容易过拟合，在数据有限时表现不如MPNNs。
计算复杂度高：全局全对注意力机制的时间复杂度和空间复杂度随节点数量呈二次增长，限制了图变换器在具有数百万节点的图上的应用。
社区结构处理困难：大规模图(如社交网络和引用网络)通常具有社区结构，这些结构具有紧密相连的组和明显的层次属性，但图变换器往往缺乏在各个层次上融入层次结构信息的能力。
方法
层次距离结构编码(HDSE)方法详解
Luokai等(2024)提出的层次距离结构编码(Hierarchical Distance Structural Encoding, HDSE)方法专门为增强图转换器在捕捉图中层次结构方面的能力而设计。以下是该方法的核心内容：
1. 图层次距离(GHD)定义

首先，论文引入了图层次距离(Graph Hierarchy Distance, GHD)作为衡量图节点之间距离的新指标，特别关注其多级层次特性：
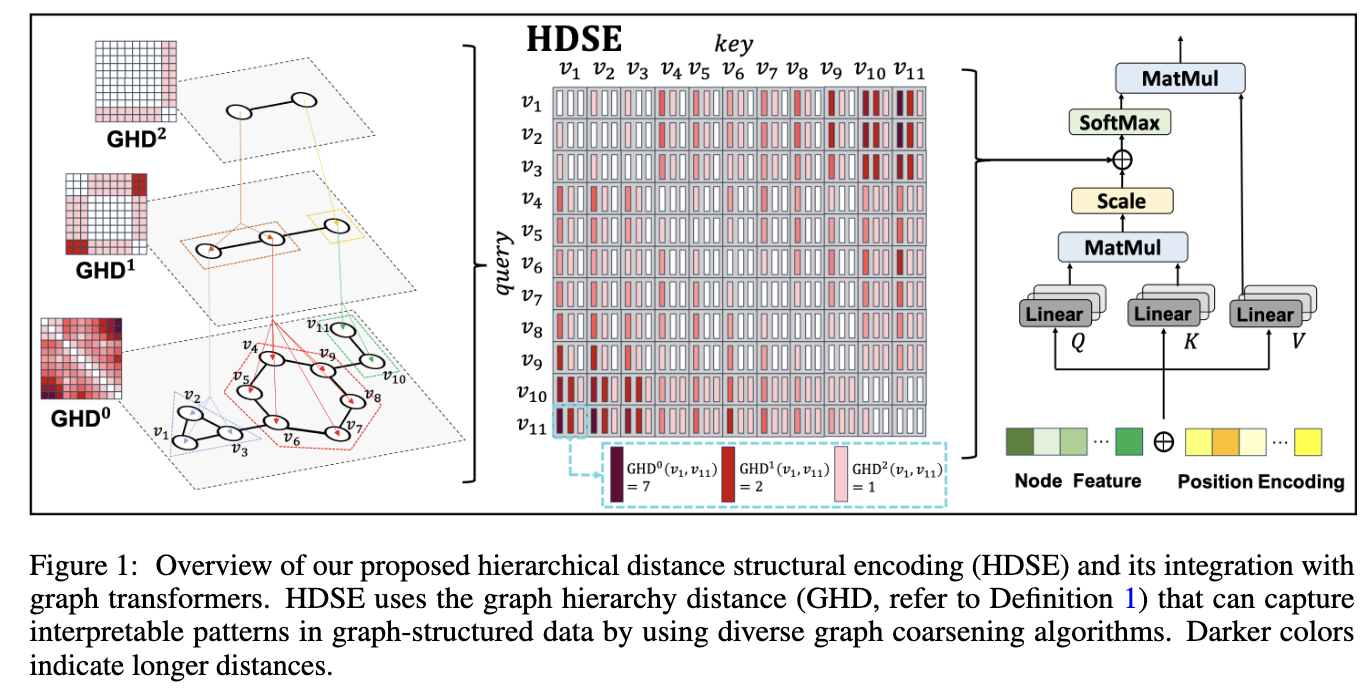
定义1（图层次距离）：给定图G中的两个节点u, v和图层次 $(G_i, \phi_i)_{i \geq 0}$ ，k级层次距离GHD定义为： $GHD_0(u, v) = SPD(u, v) \quad (2)$ $GHD_k(u, v) = SPD(\phi_{k-1} \circ \ldots \circ \phi_0(u), \phi_{k-1} \circ \ldots \circ \phi_0(v)) \quad (2)$ 其中 $SPD(\cdot, \cdot)$ 表示两个节点之间的最短路径距离（若节点不连通则为∞）， $\phi_{k-1} \circ \ldots \circ \phi_0(\cdot)$ 将 $G_0$ 中的节点映射到 $G_k$ 中的节点。
GHD满足距离度量的四个性质：零当且仅当节点相同、恒为正、对称性及三角不等式。如图1所示， $GHD_0$ $(v_1, v_{11}) = 7$ ，而 $GHD_1(v_1, v_{11}) = 2$ ，表明在更高层次上节点间的距离关系被简化，这有助于捕捉图中的层次结构。
2. 层次距离结构编码(HDSE)
基于GHD，论文提出层次距离结构编码(HDSE)，对于每对节点$i, j \in V$定义为： $D_{i,j} = [GHD_0, GHD_1, \ldots, GHD_K]_{i,j} \in \mathbb{R}^{K+1} \quad (3)$ 其中$GHD_k$是k级层次距离矩阵，$K \in \mathbb{N}$控制考虑的最大层次级别。
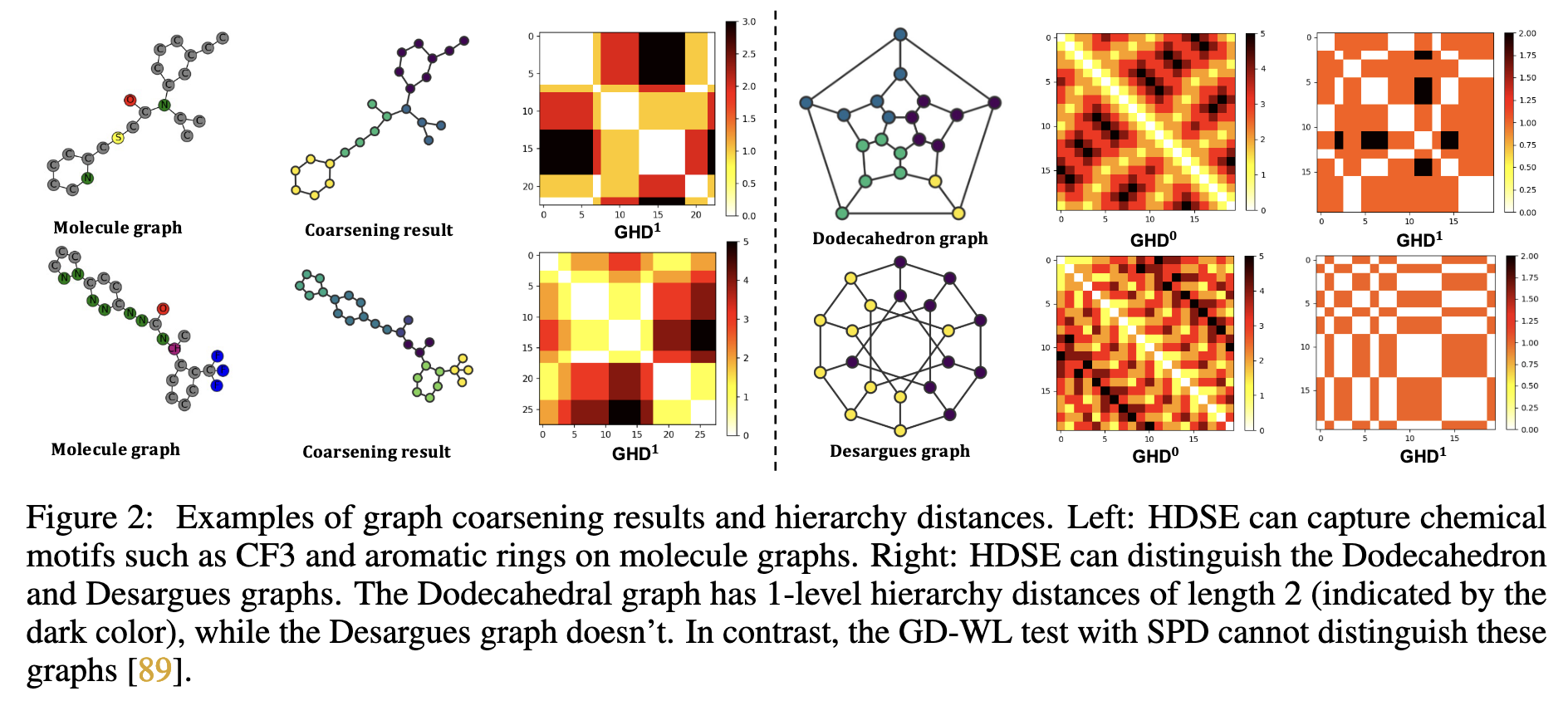
HDSE相比传统的最短路径距离(SPD)具有更强的表达能力。通过GD-WL测试可以证明，HDSE能够区分更多不同结构的图。如图2所示，HDSE可以区分立方体图(Desargues)和十二面体图(Dodecahedron)，而仅使用SPD的GD-WL测试无法区分这两个图。
3. HDSE在图转换器中的集成
为了将HDSE整合到现有图转换器的注意力机制中，论文提出了一种新颖框架：
首先，使用端到端可训练函数$\text{Bias}: \mathbb{R}^{K+1} \rightarrow \mathbb{R}$学习偏置的结构权重： $H_{i,j} = \text{MLP}\{e^0_{\text{clip}^0_{i,j}}, \ldots, e^K_{\text{clip}^K_{i,j}}\}, \quad H_{i,j} \in \mathbb{R} \quad (4)$ 其中： $\text{clip}^k_{i,j} = \min(L, GHD^k_{i,j}), \quad 0 \leq k \leq K$ 这里 $[e_0^k, e_1^k, \ldots, e_L^k]_{0\le k \le K} \in \mathbb{R}^{d \times (L+1)}$ 收集了 $L+1$ 个可学习的特征嵌入向量，分别对应 $k$ 层次的不同距离。
然后将学习到的偏置权重集成到图转换器的自注意力机制中： $\text{Attention}(X) = \text{softmax}\left(\frac{A + H}{\sqrt{d'}}\right)V, \quad A = QK^\top \quad (5)$ 这种集成方式与主干架构无关，可以无缝集成到现有图转换器的自注意力机制中。论文从理论上证明了HDSE在表达能力和泛化能力方面的优越性。
4. 大规模图的高级HDSE
对于大规模图（从百万到十亿节点），全局全对注意力机制的计算复杂性问题变得尤为突出。受Linformer的启发，论文提出了高级HDSE，将线性转换器偏向图的层次结构： $D^c_{i,j} = \left[GHD^c\left(\prod_{l=0}^{c-1} P^l\right), \ldots, GHD^K\left(\prod_{l=0}^{c-1} P^l\right)\right]_{i,j}, \quad 1 \leq c \leq K \quad (7)$ 其中：

$GHD^m$ 表示 $m$ 级图层次距离矩阵（graph hierarchy distance）
$P^l$ 是投影矩阵，每行是独热向量，表示输入节点所属的 $l$ 级集群
$\prod_{l=0}^{c-1} P^l$ 是投影矩阵的连乘积
$D^c \in \mathbb{R}^{|V^0| \times |V^c| \times (K+1-c)}$，其中 $V^0$ 是原始图的节点集，$V^c$ 是第 $c$ 级粗化图的节点集
$GHD^m\left(\prod_{l=0}^{c-1} P^l\right)$, $c \leq m \leq K$ 计算的是输入节点到c级图层次中的集群的距离

注意：

在2.1节中，论文定义了投影矩阵$P̂^k ∈ {0,1}^{|V^k|×|V^{k+1}|}$，其中$P̂^k_{ij} = 1$当且仅当在k级图中的节点$v^k_i$属于k+1级图中的节点$v^{k+1}_j$所在的簇
归一化版本的投影矩阵定义为$P^k = P̂^k C_k^{-1/2}$，其中$C_k$是对角矩阵，其对角线元素表示簇的大小
每个投影矩阵$P^l$的行是一个one-hot向量，表示输入节点属于l级的哪个簇
投影矩阵的乘积$∏_{l=0}^{c-1} P^l$代表从原始图$G^0$到高阶粗粒度图$G^c$的直接映射关系
5. 理论基础
论文从理论上证明了HDSE的优越性：
命题1：使用HDSE的GD-WL测试比使用最短路径距离SPD的GD-WL测试具有更强的表达能力。论文首先证明了GD-WL使用HDSE至少能区分GD-WL使用SPD所能区分的所有图；然后通过十二面体图和立方体图的例子展示了HDSE的更强区分能力。
命题2：具有HDSE的图转换器区分非同构图的能力至多等同于使用HDSE的GD-WL测试。在适当参数和足够多的头和层数下，具有HDSE的图转换器可以匹配使用HDSE的GD-WL测试的能力。
推论1：存在一个使用HDSE的图转换器，比使用相同架构但使用SPD或不使用相对位置编码的图转换器更具表现力。
命题3：对于半监督节点分类问题，当节点标签由”hierarchical core neighborhood”决定时，适当初始化的具有HDSE的单层图转换器能获得满意的泛化误差，而使用SPD或不使用相对位置编码无法保证这一点。
HDSE通过在图转换器中引入强归纳偏置，有效解决了transformer架构在图学习中缺乏层次结构信息的局限，在各种图任务中取得了优越的性能表现。

Metadata

摘要

研究问题

研究问题概述

方法

层次距离结构编码(HDSE)方法详解

1. 图层次距离(GHD)定义

2. 层次距离结构编码(HDSE)

3. HDSE在图转换器中的集成

4. 大规模图的高级HDSE

5. 理论基础