论文阅读:Primphormer
Metadata
- 作者: Mingzhen He, Ruikai Yang, Hanling Tian, Youmei Qiu, Xiaolin Huang
- 出处: ICML
- 日期: 2025
- PDF: https://openreview.net/pdf?id=fMAihjfJij
摘要
论文摘要翻译
图Transformer(GT)已成为图表示学习的一种有前景的方法。尽管取得了成功,但由于GT需要进行成对(pair-wise)计算,其二阶复杂度限制了在大规模图上的可扩展性。为了从根本上减少GT的计算负担,我们提出了一种原始-对偶(primal-dual)框架,将图上的自注意力机制解释为对偶表示(dual representation)。基于这一框架,我们开发出了Primphormer,这是一种高效GT,利用具有线性复杂度的原始表示(primal representation)。理论分析表明,Primphormer既是序列和图上函数的通用近似器(universal approximator),又保留了对非同构图(non-isomorphic graphs)的判别能力。在各种图基准上的广泛实验证明,Primphormer取得了具有竞争力的经验结果,同时保持了更友好的内存和计算成本。
研究问题
本文主要解决了图Transformer(GTs)在实际应用中的计算效率问题。具体研究的问题可以概括为以下几个方面:
核心问题
传统图Transformer面临二次方(O(N²))的计算复杂度,这是由于其自注意力机制中需要计算每对节点之间的相似度,导致在大规模图上的可扩展性受到严重限制。
现有解决方案的局限性
作者分析了之前解决这一问题的方法及其不足:
- 线性注意力模型:如Performer和BigBird虽然减少了计算复杂度,但引入了额外的计算开销,成为中等规模图的主要计算瓶颈
- 稀疏注意力机制:如Exphormer利用图结构的稀疏性,但当图变得更密集时,复杂度又退化为二次方
- 序列特定方法:如Primal-Atten等方法虽然解决了序列数据中的表示问题,但不适用于图数据,因为图中的节点没有自然顺序属性
理论挑战
关键的技术挑战是注意力分数本身具有非对称性(κ(x,y)≠κ(y,x)),这违反了Mercer条件,使得经典的原始-对偶讨论无法直接应用。虽然最近的研究已经在探索不对称核机器中的原始-对偶关系,但这些方法主要是在序列数据上设计的,不适用于图网络。创新切入点
为了从根本上增强GTs的可扩展性,作者寻求避免成对(pair-wise)计算的方法,从核机器中的原始-对偶关系获取灵感。他们注意到传统的支持向量机(Cortes & Vapnik, 1995)、最小二乘支持向量机(Suykens & Vandewalle, 1999)和核主成分分析(Mika et al., 1999)等模型展示了如何通过在原始空间中表示来避免二次复杂度。针对图数据的具体挑战
对于图数据应用原始-对偶关系时,作者遇到了一个基本问题:与不同节点对上的序列不同,图中的节点没有明确指定的顺序或排列,这使得讨论图上自注意力的原始-对偶关系成为一个开放性问题。
综上所述,本文主要研究问题是如何开发一种高效的图Transformer架构,它能够: - 规避成对计算,将计算复杂度从二次方降低到线性
- 保留区分非同构图的表达能力
- 在保证性能的同时,提供更友好的内存和计算成本Primphormer的研究问题主要集中在解决图Transformer在处理大规模图时的计算效率限制。传统图Transformer(GTs)由于自注意力机制中的成对(pair-wise)计算,具有二次方(O(N²))的计算复杂度,这严重限制了它们在大规模图上的可扩展性。
方法
引言
He等人(2025) 提出的Primphormer旨在解决图Transformer(GTs)在大规模图应用中的计算效率问题。传统GTs的自注意力机制由于需要进行成对计算,导致计算复杂度为O(N²),严重限制了其在大型图上的可扩展性。为解决这一问题,作者提出了一种基于原始表示(primal representation)的框架,通过原始-对偶关系将自注意力机制重构为线性复杂度模型,同时保持模型的表达能力。Primphormer核心方法
1. 问题与动机
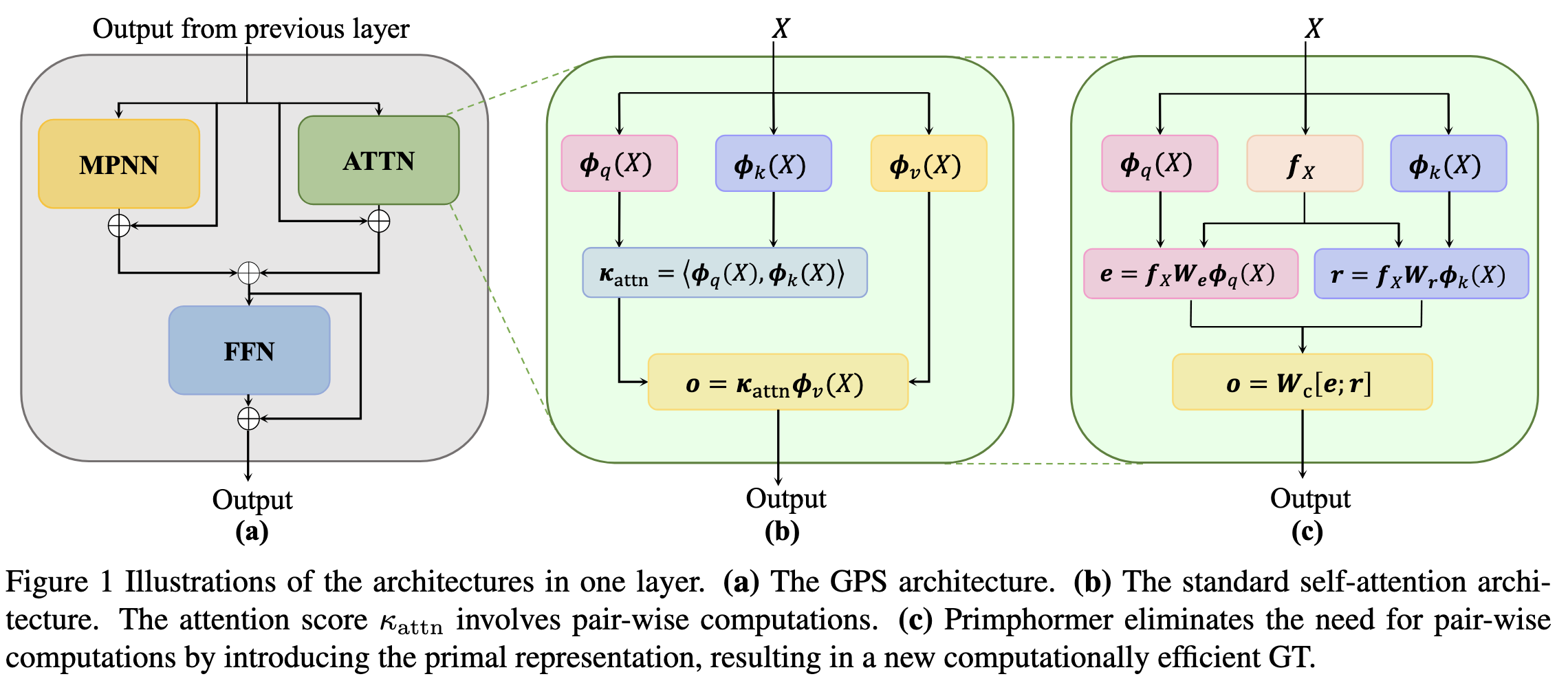
图Transformer在处理长程依赖时表现出色,但其自注意力机制需要计算所有节点对之间的注意力分数:其中$q(\cdot)$、$k(\cdot)$和$v(\cdot)$分别是查询(query)、键(key)和值(value)的投影函数,$\sigma$是激活函数。这种成对计算导致$O(N²)$复杂度,限制了实际应用。2. 原始-对偶框架
论文引入核机器中的原始-对偶关系,将自注意力机制解释为对偶表示,并通过空间转换实现原始表示:2.1 不对称核技巧
由于注意力分数$\kappa(x, y) \neq \kappa(y, x)$违反Mercer条件,作者采用定义2.1的不对称核技巧:其中$\phi_q$和$\phi_k$是查询和键的特征映射。2.2 虚拟节点与全局聚合
为保持图的置换等变性,引入虚拟节点,其中:
- $B, F$是可学习权重
- $X_1^N$是节点特征矩阵
- $1_{N_s}$是长度为$N_s$的全1向量($N_s \ll N$)
公式详细理解见附录A.2.3 优化问题构建
基于原始表示定义优化问题:约束条件:其中$\Theta = {W_e, W_r, e_i, r_j}$是参数集,$\Lambda$是对角正则化矩阵,$W_e, W_r \in \mathbb{R}^{N_s \times p}$。
此优化问题本质是进行正则化,对于变分原理优化及KKT条件,见附录D.2.4 对偶问题与原始表示
定理2.2的KKT条件给出对偶问题:通过优化推导出原始表示与对偶表示的关系: - 原始表示:
- 对偶表示:其中和形成数据自适应基。
对于优化问题的详细推导和理解见附录B2.5 输出
得到$e$(查询特征映射)和$r$(键特征映射)后,采用拼接进行输出:3. 实现与架构
Primphormer模型架构为$T_{Pri} = \text{FFN}(X + \text{Prim}(X))$,其中:
- 定理3.2:Primphormer是置换等序列函数的通用近似器
- 定理3.3:添加位置编码后,Primphormer可近似任意连续序列函数
2. 表达能力保留
- 定理3.4:Primphormer能模拟1-Weisfeiler-Lehman(1-WL)测试,证明其与标准Transformer区分非同构图的能力相当:
实验结果
Primphormer在多个基准数据集上验证了其高效性与有效性:
- LRGB数据集(表1):在5个数据集中,Primphormer在4个上超越基线
- GNN基准(表2):在MNIST上达到98.56%准确率,优于其他GT模型
- 效率对比(表4):计算复杂度从O(N²)降至O(Nps),内存占用显著降低,例如在MalNet-Tiny上仅需2.86GB(远低于Exphormer的10.38GB)
总结
Primphormer通过以下创新解决了GTs的计算效率问题: - 引入原始-对偶框架,将二次复杂度转换为线性复杂度
- 设计虚拟节点机制保持图的置换等变性
- 理论证明其通用近似能力和表达能力
- 实验验证在保持性能的同时大幅降低计算和内存开销
这一方法为图Transformer在大规模图上的应用提供了新思路,未来可进一步探索边特征集成和高效微调方法。
参考:
He, M., Yang, R., Tian, H., Qiu, Y., & Huang, X. (2025). Primphormer: Efficient Graph Transformers with Primal Representations. Proceedings of the 42nd International Conference on Machine Learning.
附录
附录A
在论文的Primphormer模型中,虚拟节点全局聚合机制是通过平均池化后经过可学习的线性层实现的,具体分析如下:
虚拟节点的实现方式
从论文第2.3节的定义可以看到,虚拟节点被定义为:其中:
- $F \in \mathbb{R}^{s \times N_s}$ 和 $B \in \mathbb{R}^{s \times d}$ 是可学习权重
- $X_1^N \in \mathbb{R}^{d \times N}$ 是节点特征矩阵
- $1_{N_s}$ 是长度为 $N_s$ 的全1向量
数学表达
结合理论和代码,虚拟节点的聚合过程可以表示为: $f_X^{(l+1)} = \text{FFN}(\text{global_mean_pool}(h^{(l)})) + f_X^{(l)}$ 其中: - global_mean_pool() 是平均池化操作
- FFN() 代表一个可学习的线性层
- $f_X^{(l)}$ 是第 $l$ 层的虚拟节点表示
附录B
本文提出的优化问题在公式(2.5)中定义如下:
约束条件为:
为什么公式这样构建
这个优化问题的构建基于以下几个关键原因:
- 处理自注意力的不对称性:传统图Transformer中的自注意力机制是$O(N²)$复杂度的且存在不对称性,违反了Mercer条件。该优化问题通过引入变分原理,使Primphormer能够处理非对称核。
- 保持置换等变性:通过虚拟节点$f_X$聚合全局信息,保证图神经网络所需的置换等变性,这对于无序的图数据至关重要。
- 降低计算复杂度:通过在原始空间中进行优化,避免了传统自注意力机制中需要计算所有节点对的问题。
- 形成数据自适应基:通过将全局信息整合到投影权重中,而非特征映射中,构建双空间中的数据自适应基,增强了模型灵活性。(因此使用参数矩阵构建,而不是采用全局信息与特征输出相加)
各项含义
目标函数$J$中的各项含义如下:
- 正则化项:
- 这两项是对投影得分$e_i$和$r_j$的正则化,通过正定矩阵$\Lambda$防止过拟合
- $\Lambda$是对角正则化系数矩阵,控制不同维度上的正则化强度
- 迹项:$-\text{Tr}(W_e^\top W_r)$
- 这一项鼓励$W_e$和$W_r$之间的一致性
- 在KKT条件下,当满足优化条件时,与前两项达到平衡
- 约束条件中的参数:
- $W_e, W_r \in \mathbb{R}^{N_s \times p}$:可学习权重矩阵,其中$N_s \ll N$
- $e_i, r_j \in \mathbb{R}^s$:投影得分
- $\phi_q(\cdot), \phi_k(\cdot) : \mathbb{R}^d \to \mathbb{R}^p$:查询和键的特征映射
- :数据依赖投影,定义为,作为虚拟节点聚合全局信息
数学推导
数学推导过程主要包括以下步骤:
1. 拉格朗日函数
首先构建拉格朗日函数:
其中$h_e^i, h_r^j \in \mathbb{R}^s$是与投影得分$e_i$和$r_j$相关的对偶变量向量。
2. KKT条件
通过对拉格朗日函数求偏导,得到KKT条件:
3. 对偶问题
通过消除原始变量$W_e$和$W_r$,可以得到以下广义特征值问题:
其中是自相关矩阵,和是对偶变量,,是由注意力分数诱导的核矩阵。
4. 原始表示与对偶表示
基于KKT条件,论文推导出自注意力的原始表示和对偶表示:
原始表示:
对偶表示:
其中$F_X := f_X f_X^\top$包含全局信息,$\tilde{h}_r^j := F_X h_r^j$和$\tilde{h}_e^i := F_X h_e^i$是数据自适应基,$\kappa(x_i, x_j) := \langle \phi_q(x_i), \phi_k(x_j) \rangle$是核函数。
5. 零值目标引理
论文证明了在对偶空间中满足KKT条件的解会导致原始空间中的目标值为零(引理2.3):
这一结果为后续实现提供了理论基础,使得Primphormer可以通过简单地将原始目标值作为额外损失项来优化,而不需要直接求解复杂的对偶问题。
通过这种优化设计和推导,Primphormer能够高效地实现图Transformer,避免O(N²)的复杂度,同时保持置换等变性和表达能力。
附录C
根据Primphormer论文中的定义,满足置换等变性后,节点重新排序不影响输出值,只是输出的排列顺序也会相应变化。
置换等变性的正式定义
论文中给出了置换等变性的明确定义(定义3.1):
一个连续的序列到序列函数 $f: X^N \to Y^N$ 如果对于每个排列 $\pi: [N] \to [N]$ 满足以下条件,则称其对序列中元素的顺序具有等变性:
其中 $X = [x_1, \ldots, x_N]$ 是包含 $N$ 个令牌的序列。
对图神经网络的重要性
论文特别强调了图数据中置换等变性的重要性:
“First, unlike sequences, nodes in a graph are unordered, meaning the sampling operation may break permutation equivariance, i.e., any permutation of the nodes could result in a different output.”
这是因为图中的节点本质上是无序的(unlike sequences),与序列数据不同。如果图神经网络不具有置换等变性,那么当对节点进行不同的排序时,可能会得到不一致的输出结果,这与图结构的基本特性相违背。
Primphormer如何保持置换等变性
论文指出,Primphormer通过引入虚拟节点(virtual node)机制来保持置换等变性:
“We collect graph information by introducing a virtual node (Cai et al., 2023) that aggregates global information.”
“The global aggregationpreserves permutation equivariance.”
这种全局聚合方式本质上是一个对称操作,对节点排列保持不变,从而确保了模型对节点重排的不变性。
结论
“满足置换等变性后节点重新排序不影响输出”的理解是正确的。更准确地说,满足置换等变性意味着:
- 当输入序列中的元素进行重新排列时,输出序列也会以相同的方式进行排列
- 输出序列中元素本身的值不会发生改变
- 对于图神经网络,这意味着无论图中节点的顺序如何变化,只要图的结构(边和节点特征)保持不变,模型的处理结果就会保持一致
这一性质对于图神经网络至关重要,因为它尊重了图作为无序数据结构的基本特性。
附录D
KKT条件(Karush-Kuhn-Tucker条件)是优化理论中的一组重要条件,用于解决约束优化问题。这些条件是由Karush (1939)、Kuhn和Tucker (1951)提出的,是非线性规划领域中求解约束优化问题最优解的必要条件。
在Primphormer论文中的应用
在He等(2025)的论文中,KKT条件被用来建立优化问题(2.5)的对偶问题,这是Primphormer理论基础的关键部分。论文中定义了原始优化问题的拉格朗日函数:
通过求拉格朗日函数的偏导数并设为零,论文得到了KKT条件:
KKT条件的主要内容
KKT条件通常包括:
- 原始可行性条件:满足原始问题的约束条件
- 对偶可行性条件:满足对偶变量的符号约束(对于不等式约束)
- 互补松弛条件:原始约束和对应的对偶变量的乘积为零
- 梯度条件:原始问题和对偶问题的梯度条件
在Primphormer中的意义
其中Σ = Λ⁻¹,He和Hr是对偶变量,K是由注意力分数形成的矩阵。这种原始-对偶关系证明了Primphormer的自注意力机制可以通过原始表示有效实现,同时避免了二次复杂度计算。
KKT条件在Primphormer中不仅为理论证明提供了基础,还在实际实现中起到了指导作用(引理2.3表明,当达到KKT点时,原始空间的目标函数值为零)。
附录E
论文中提出的定理
定理 2.2 (Duality)
He 等 (2025) 提出的这个定理描述了优化问题 (2.5) 在 KKT 条件下的对偶问题,即:
其中 $\Sigma = \Lambda^{-1}$,$H_e$ 和 $H_r$ 是对偶变量,$K$ 是由注意力分数诱导的矩阵。该定理建立了原始空间(Primal)与对偶空间(Dual)之间的关系,证明了 Primphormer 可以通过原始表示实现,从而避免二次复杂度计算。
引理 2.3 (Zero-valued objective with stationary solutions)
该引理指出,在对偶空间 (2.6) 中 $H_e, H_r, \Sigma$ 的解会导致原始空间 (2.5) 中目标值 $J$ 为零。这个结果支持了 Primphormer 的实现方式:通过最小化额外的目标损失函数有效逼近 KKT 点。
定理2.3的证明
定理2.3(引理2.3)表明:对偶空间(2.6)中He、Hr、Σ的解会导致原始空间(2.5)中目标值J为零。
证明过程
根据KKT条件(C2)和优化问题(2.6),目标函数在平稳点上的值为:
根据KKT条件中的和,我们有:
令 $Σ = Λ^{-1}$ ,则上式可写为:
根据KKT条件中的和,我们可以将迹项展开:
其中,。
定义注意力矩阵 $K$,其中 $K_{ij} = ⟨φ_q(x_i), φ_k(x_j)⟩ = φ_q(x_i)^T φ_k(x_j)$,则:
其中 $F_X = f_X f_X^T$ 。由于 $KH_r F_X = H_e Σ$ 和 $K^T H_e F_X = H_r Σ$ ,我们可以将 $J$ 重写为:
简化后:
对于任何矩阵 $M$ ,都有 $Tr[M - M^T] = 0$ ,因为 $M - M^T$ 是斜对称矩阵,其迹为零。
结论
因此,我们证明了:在对偶空间(2.6)中 $H_e$、$H_r$ 、$Σ$ 的解会导致原始空间(2.5)中目标值 $J$ 为零。这个结果支持了Primphormer的实现方式:通过最小化额外的目标损失函数有效逼近KKT点。
定理 3.2 (Universal approximation for permutation equivariant sequence-to-sequence functions)
该定理证明了 Primphormer 作为置换等变序列函数的通用逼近器:
对于任意函数和每个,存在一个 Primphormer,使得
证明
我们将证明分为两个部分:首先用Sumformer逼近f,然后用Primphormer逼近Sumformer。证明基于三角不等式:
第一步:用Sumformer逼近f
根据引理C.2(Alberti等, 2023):
引理C.2:对于每个函数 $f ∈ Fe^N_q(X, Y)$ 和每个 $ε > 0$ ,存在一个Sumformer S,使得
我们选择一个Sumformer S,使得。Sumformer的定义如下:
定义C.1(Sumformer):设d’ ∈ N且有两个函数,。Sumformer是一个序列到序列函数,首先计算:
然后,$S([x_1, …, x_N]) := [ψ(x_1, Ξ), …, ψ(x_N, Ξ)]$ 。
第二步:用Primphormer逼近Sumformer
现在我们构造一个Primphormer $T_{Pri}$ 来近似Sumformer S:
- 首先将输入X通过前馈层变换:
- 构造一个两层前馈网络,在前N个分量上执行恒等变换,同时近似函数ξ:
- 添加线性映射产生输出:
使用注意力机制表示 $Ξ = ∑_{i=1}^N ξ(x_i)$ :
- 设置 $W_q = W_k = [e_1, 0^{(1+d+2d’)×(d+2d’)}]$ ,其中 $e_1 = [1, 0^{1×(d+2d’)}]^T$
- 数据依赖投影,其中
- 得到投影分数:$[Ξ, …, Ξ] ∈ R^{d’×N}$
连接投影分数并通过兼容矩阵 $W_c$ 产生最终输出,应用残差连接:
通过这种架构,Primphormer的注意力模块被设计用来计算Sumformer的聚合,而其余部分保持不变。因此,我们可以构造Primphormer,使得。
结论
利用三角不等式,我们得到:
这就完成了定理3.2的证明,表明Primphormer是置换等变序列到序列函数的通用逼近器。
值得注意的是,证明的关键在于将问题分解为两个可管理的部分,并分别用Sumformer和Primphormer的通用逼近性质来实现整体近似。这种方法受到Alberti等(2023)工作的启发,并结合了Primphormer的特定架构特性。
定理 3.3 (Universal approximation for arbitrary continuous sequence functions)
该定理证明带有位置编码的 Primphormer 能近似任意连续序列函数:
对于任意连续函数 $f : [0,1]^{d \times N} \rightarrow \mathbb{R}^{d \times N}$ 和每个 $\varepsilon > 0$,存在一个带有位置编码 $E$ 的 Primphormer $T^{PE}$,使得
证明
第一步:引入位置编码与分片常数函数近似
由于目标函数 $f$ 是连续的,其分量函数也是连续的。考虑作为紧致集,在紧集上一致连续。给定,存在使得当时,有。
定义网格:
将空间划分为超立方体网格,其中。构造分片常数函数:
由于g的一致连续性,对于足够小的δ,有:
引入位置编码:
使得X+E的第k个列向量位于区间[k-1, k)内,不同token位于互不相交的区间。
第二步:构建Sumformer S
定义映射 $l: R^d → R$ ,对于列向量 $H_i ∈ R^d$:
该映射将不同列映射到不同区间:,且对任意排列π满足。
利用Kolmogorov-Arnold表示定理(Khesin & Tabachnikov, 2014),定义从位置标识到网格索引的函数:
其中和是连续函数。
定义聚合函数:
并定义:
其中将网格点分解为当前token与其他token,χ将网格点映射到位置标识b。
构建Sumformer S:
由于精确表示网格点上的值且位置编码保持顺序,有:
第三步:用Primphormer逼近Sumformer
根据定理3.2的证明思路(Alberti等, 2023),Primphormer可以逼近置换等变函数。尽管此处S不是置换等变的,但位置编码E固定了顺序,使得:
其中 $T_{Pri}$ 为Primphormer,通过以下方式构建:
- 前馈变换:$[x_1 \cdots x_N; x_1 \cdots x_N] \in R^{2d \times N}$
- 两层前馈网络保持前N个分量不变,同时近似ξ函数
- 添加线性映射与数据依赖投影计算$\Xi = \sum_{i=1}^N \xi(x_i)$
- 通过兼容矩阵 $W_c$ 输出最终结果
第四步:整合结果
由三角不等式:其中。结论
定理3.3证明完成:对于任意连续函数f和ε > 0,存在位置编码E和Primphormer TPE,使得在 $[0,1]^{d×N}$ 上一致逼近f的误差小于ε。这一结果证明了Primphormer在添加适当位置编码后,可以作为任意连续序列到序列函数的通用逼近器(Alberti等, 2023)。定理 3.4 (Expressiveness in terms of 1-WL)
该定理证明了 Primphormer 的表达能力与 1 维 Weisfeiler-Lehman 算法(1-WL)相当:
设 $G = (V, E, l)$ 是有 $N$ 个节点的标记图,节点特征矩阵 $X^{(0)} := H \in \mathbb{R}^{d \times N}$ 与标签 $l$ 一致。那么对于所有迭代 $t \geq 0$,存在 Primphormer 的参数化,使得对于所有节点 $v, w \in V$,其中 $C^t_{1}$ 是 1-WL 测试在第 $t$ 次迭代中的着色函数。证明
1. 初始化
根据引理C.7,存在一个初始化$X^{(0)}$的参数化,使得对于每个顶点$v \in V$:并且满足:其中$d = 2s + r + k$。我们使用归纳法进行证明。
首先,根据1-WL测试的定义,我们有:令$H^{(t)}(v)$表示迭代$t$时节点$v$的颜色表示。设$D^{\text{emb}} \in \mathbb{R}^{r\times N}$,使得对于第$i$列$D^{\text{emb}}_i = \deg’(v_i)$,其中$v_i$是某个固定但任意的节点排序中的第$i$个节点。那么$X^{(0)}$可以写为:2. 归纳假设
假设命题在迭代$t$时成立,即存在Primphormer的参数化,使得:现在我们证明命题在$t+1$时也成立。为此,我们需要:这意味着$X^{(t+1)}$的第一个元素应该匹配1-WL等价的聚合:3. 1-WL等价聚合
根据引理C.4,我们知道1-WL等价聚合遵循:其中$\text{FFN}_{\text{WL}}$是更新颜色的前馈层。因此,我们需要证明Primphormer能够模拟这一聚合过程。4. Primphormer参数化
考虑Primphormer的输出$o(x) = W_c [e(x); r(x)]$,其中:通过适当设置参数,我们可以将Primphormer参数化为$o(x) = e(x) = W_e \phi_q(x)$。设$\phi_q(x) := q(x)/|q(x)|_2$和$\phi_k(x) := k(x)/|k(x)|_2$,其中$q(x) = W_qx$和$k(x) = W_kx$。
将$W_q$和$W_k$进行分解:其中子矩阵维度分别为,,,。
根据KKT条件,我们可以在行空间中重新参数化:其中$H$是一个由权重向量构成的矩阵。因此,Primphormer的输出可以表示为:5. 模拟图拉普拉斯算子
通过设置合适的参数,我们可以使Primphormer模拟图拉普拉斯算子的作用。根据引理C.7,结构嵌入$P’$可以恢复(归一化)图拉普拉斯算子,即$P’^\top P’ = L$。
经过一系列变换,Primphormer的输出可以重写为:其中$L = D - A$是图拉普拉斯算子,$D$是度矩阵,$A$是邻接矩阵。6. 完成归纳步骤
最后,我们得到Primphormer的输出为:结合模型结构 $\text{FFN}(X + \text{Prim}(X))$ ,Primphormer计算下一个表示:通过定义合适的函数,我们可以使Primphormer精确地模拟1-WL的聚合过程,得到:其中$H^{(t+1)} = \text{FFN}_{\text{WL}}[H^{(t)} + 2H^{(t)}A(G)]$正是1-WL测试在第$t+1$次迭代的特征。
因此,我们证明了存在Primphormer的参数化,使得:根据引理C.5和定理C.8,我们知道Transformer和Primphormer在区分非同构图方面都能够模拟1-WL测试,表明了Primphormer保持了与标准Transformer相同的表达能力。推论 3.5 (Expressiveness comparison with Transformer)
该推论是定理 3.4 的延伸,指出 Transformer 和 Primphormer 在区分非同构图方面具有相同的表达能力:
设 $G = (V, E, l)$ 是有 $N$ 个节点的标记图,节点特征矩阵 $X^{(0)} := H \in \mathbb{R}^{d \times N}$ 与标签 $l$ 一致。那么对于所有迭代 $t \geq 0$,存在 Transformer 和 Primphormer 的参数化以及位置编码,使得对于所有节点 $v, w \in V$。论文中引用的其他重要定理
定义 2.1 (Asymmetric kernel trick)
引用自 Wright & Gonzalez (2021) 、Lin et al. (2022) 、He et al. (2023a) 和 Chen et al. (2023) ,定义了来自再生核巴拿赫空间(RKBS)的非对称核技巧:表示定理 (Representer theorem)
引用自 Kimeldorf & Wahba (1971) ,描述了原始空间和对偶空间之间的最优解关系:引理 C.2 (Universal approximation of Sumformer)
引用自 Alberti et al. (2023) ,证明了 Sumformer 可以作为置换等变函数的通用逼近器。引理 C.3 (Kolmogorov-Arnold representation)
引用自 Khesin & Tabachnikov (2014) 和 Zaheer et al. (2017) ,证明了任意多元连续函数有特定表示形式:引理 C.4 (Theorem VIII.4 in Grohe, 2021)
引用自 Grohe (2021) ,说明了 GNN 如何模拟 1-WL 测试过程。引理 C.5 (Theorem 2 in Müller & Morris, 2024)
引用自 Müller & Morris (2024) ,证明了标准 Graph Transformer 可以模拟 1-WL 测试。定义 C.6 (LAP and SPE)
引用自 Kreuzer et al. (2021) 和 Huang et al. (2024) ,定义了两种结构嵌入方法:
- LAP: $\psi(V^T_1, \lambda), \cdots, \psi(V^T_N, \lambda)$
- SPE: $V \varphi_1(\lambda) V^T, \cdots, V \varphi_m(\lambda) V^T$